144. Binary Tree Preorder Traversal

Source
Topic: Array, Prefix Sum

Given the root of a binary tree, return the preorder traversal of its nodes' values.

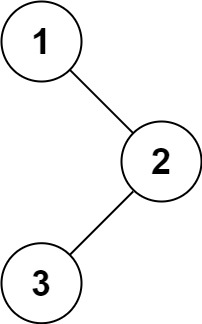
Input: root = [1,null,2,3] Output: [1,2,3]

Constraints

• The number of nodes in the tree is in the range [0, 100].
• -100 <= Node.val <= 100

Concept

Preorder traversal of a binary tree involves visiting the root node first, followed by its left and right nodes.
This traversal can be implemented recursively by visiting each node and then recursively visiting its left and right subtrees if they are not null.

Complexity

Time Complexity

O(n) * The code performs a preorder traversal of the binary tree recursively. * At each node, the code does constant-time operations such as adding the node's value to the result vector and checking if the node has left or right children. * The code visits each node exactly once, and the work done at each node is constant time. * Therefore, the overall time complexity is proportional to the number of nodes in the binary tree, which is O(n), where n is the number of nodes.

Space Complexity

O(n)

Special test case

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> ans;

    vector<int> preorderTraversal(TreeNode* root) {

        if (root == nullptr)
            return {};

        ans.push_back(root->val);

        if (root->left != nullptr)
            preorderTraversal(root->left);

        if (root->right != nullptr)
            preorderTraversal(root->right);

        return ans;
    }
};